Welcome to the Time Management Bureau !

We need to calibrate some clocks that are affected by time floods. There is a row of $n$ clocks to be calibrated here, with the scale on each clock starting from $0$ and placed clockwise at $1,2$...... Each clock provides two numbers $x$ and $y$ to indicate that it needs to rotate $x$ times to complete one revolution and has already completed $y$ rotations from the $0$ scale.

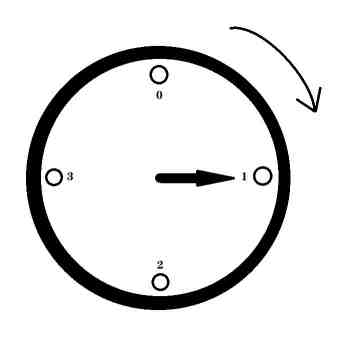
We have the three calibration operations:

• For each $i\in[1,n]$, let $y_{i} = [y_{i} \& (y_{i} + 1)] \mod x_{i} $.
• For each $i\in[1,n]$, let $y_{i} = [y_{i} \oplus (y_{i} + 1)] \mod x_{i}$.
• For each $i\in[1,n]$, let $y_{i} = (y_{i} + 1) \mod x_{i}$.

Here & denotes the bitwise AND operation, and $\oplus$ denotes the bitwise XOR operation.

The Time Management Bureau needs to calibrate these n clocks to the correct scale through several operations. But to save time, please calculate the minimum number of operations to calibrate these n clocks to the correct scale.

Output $-1$ when there is no solution.

The first line contains one positive integer $n (1 \le n \le 40)$.

The second line contains $n$ positive integers separated by spaces to represent the correct scale sequence, ensuring that the sequence is legal.

The next n lines, each contains two positive integers $x (2 \le x \le 4)$ and $y (0\le y\le x-1)$ separated by spaces.

The output contains an integer representing the minimum number of operations to calibrate all clocks.

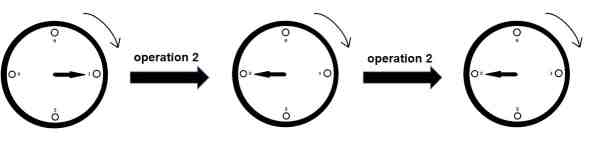
In the first test case, let's first perform operation $1$ and then operation $2$:

Scale sequence after completing operation $1$: $0,0,0,2,2$

Scale sequence after completing operation $2$: $1,1,1,1,1$