$N$ ants move along the number axis with a length of $L$. Starting from their initial position, some of them move to the right (positive direction) and some move to the left (negative direction). They move at the same speed, with a length of 1 second per unit. If they meet halfway and change their direction (instantly), turn around and walk. The position markers on the number axis are from $0$ to $L$, and ants will not stop their Long March until they reach position $0$ or position $L$.

For example:

The initial position of three ants is $3$, $5$, and $9$, with the first two facing positive and the last one facing negative,where $L$ is $10$. Two seconds later, the second ant and the third ant met at position $7$. The second ant changed direction to negative and the third ant changed direction to positive. After another second, the first ant and the second ant met at position $6$. The first ant changed direction to negative and the second ant changed direction to positive. The third ant ends its Long March at $5$ seconds (from the beginning), the second ant ends its Long March at $7$ seconds (from the beginning), and the first ant ends its Long March at $9$ seconds (from the beginning).

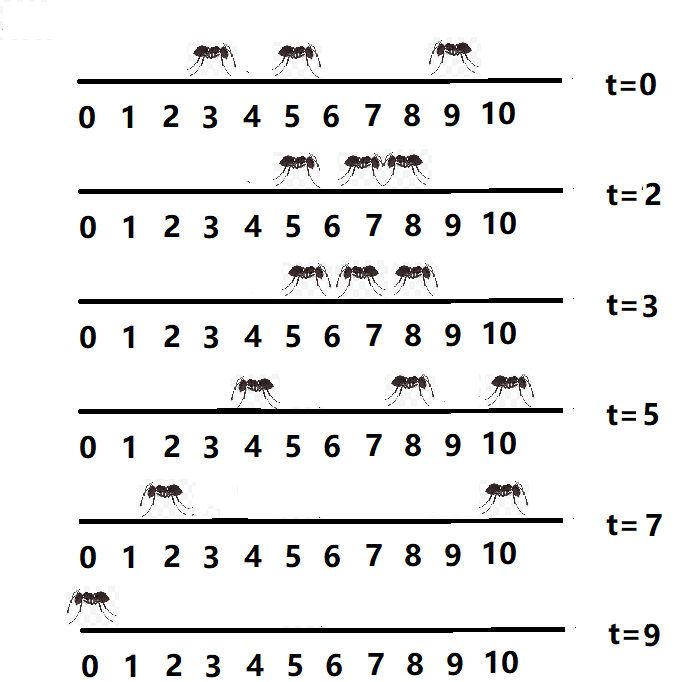
Now the initial position and direction of each ant are given. Ask the time when the last ant to complete the Long March.

The first line contains a integer $T$ indicating the number of testcases.

For each test case, there are two lines with the first line containing two positive integers $N$ and $L$, representing $N$ ants and the length of the number axis. $(N \le 10,000, L \le 1,000,000,000, N \lt L)$.

The next line contains $N$ integers $p_i (1 \le i \le N, 0 < |p_i| \lt L)$, representing the initial position and direction of the $i$-th ant.

If $p_i$ is a positive integer, it indicates that the initial position $p_i$ and initial direction of the $i$-th ant are positive.

If $p_i$ is a negative integer, it indicates that the initial position $- p_i$ and initial direction of the $i$-th ant are negative.

No two ants have the same initial position. There is no initial position for ants at the end position.

For each test case, output the time when the last ant to complete the Long March.