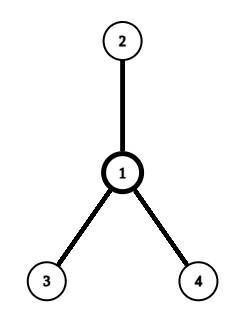
一个鸡爪是由 4 个部分组成，一个点与三个与该点相邻的边，三个边的另一端点被认为不在鸡爪中。

一个图上的鸡爪数是该图最多成形成几个鸡爪，使得图上每个点与边最多在一个鸡爪中（注意上文点与边是否在鸡爪中的定义）。

现在给你 $n$ 条边，你可以使用任意个点，构造一个简单无向图（没有自环重边），要求最大化该图的鸡爪数，并输出$n$条边的两端点。如果有多解，请让输出的 $2n$ 个数字在行优先遍历的顺序下，字典序最小。

字典序：序列$A$的字典序小于序列$B$，当且仅当存在$i (1≤i≤n)$，使得$A[i] \lt B[i]$，且对任意的$j (1≤j \lt i)$，$A[j]=B[j]$。

第一行为一个整数 $T(1≤T≤10^4)$ ，表示测试样例个数。

每个样例一行，为一个整数 $n(1≤n≤10^4)$。保证所有样例的$n$的和$≤10^4$。

每个样例输出 $n$ 行，每行两个正整数，表示该无向边连接的两个顶点（顶点从 $1$ 开始编号）。