Alice作为德鲁伊，有一棵神奇的树，这棵树会不断的成长。

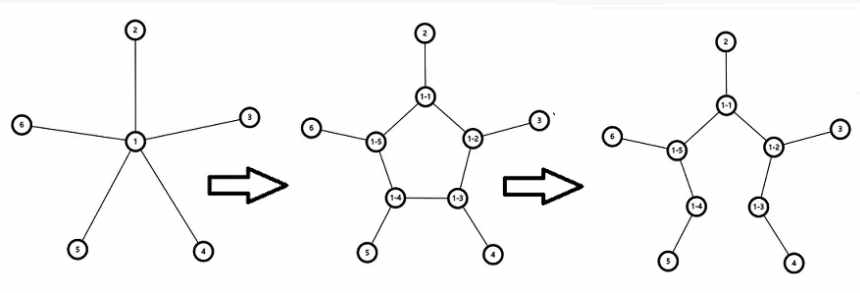
对于一个节点$i$的成长，先将这个节点变为$d_i$边型（$d_i$为这个点的度数），然后将原本与这个点相连的边随机匹配多边形上的点，再随机删除由这个点变化成的多边形上的一条边。

特别的，对于一个度数为$0$或$1$的点，进行成长将不会发生变化。

对于一棵树的成长，定义为树上所有的节点进行一次成长。

Alice认为一棵树的直径越长，长得越好，所以Alice想要知道，在这棵树进行$m$次成长后，直径的长度最大可能是多少。

这里定义树的直径的长度为直径上的点数。

答案对$10^9+7$取模。

第一行包含一个整数$T（1≤T≤5）$，表示数据组数

每组数据的第一行包含两个整数$n,m（1≤n≤10^5,1≤m≤10^9）$，表示一棵$n$个节点的树，进行$m$次成长

接下来$n−1$行，每行包含两个整数$u,v（1≤u,v≤n）$，表示树上的一条边。

一共$T$行，每行一个整数，表示第$i$棵树成长后的最大直径。