Sherlock found a piece of encrypted data which he thinks will be useful to catch Moriarty. The encrypted data consists of two integer l and r. He noticed that these integers were in hexadecimal form.He takes each of the integers from l to r, and performs the following operations: He lists the distinct digits present in the given number. For example: for 101416, he lists the digits as 1,0,4. Then he sums respective powers of two for each digit listed in the step above. Like in the above example sum=21+20+24=1910. He changes the initial number by applying bitwise xor of the initial number and the sum. Example: 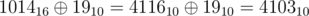. Note that xor is done in binary notation. One more example: for integer 1e the sum is sum=21+214. Letters a, b, c, d, e, f denote hexadecimal digits 10, 11, 12, 13, 14, 15, respertively.Sherlock wants to count the numbers in the range from l to r (both inclusive) which decrease on application of the above four steps. He wants you to answer his q queries for different l and r.

Input First line contains the integer q (1 \le q \le 10000).Each of the next q lines contain two hexadecimal integers l and r (0 \le l \le r \lt 1615).The hexadecimal integers are written using digits from 0 to 9 and/or lowercase English letters a, b, c, d, e, f.The hexadecimal integers do not contain extra leading zeros.

Output Output q lines, i-th line contains answer to the i-th query (in decimal notation).

For the second input,1416=2010sum=21+24=18 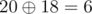Thus, it reduces. And, we can verify that it is the only number in range 1 to 1e that reduces.