Polycarp is a regular customer at the restaurant "Ber Patio". He likes having lunches there.

"Ber Patio" has special discount program for regular customers. A customer can collect bonuses and partially cover expenses in the restaurant.

Let's assume a customer currently has b bonuses and she has to pay r burles for a lunch. In this case the customer can use bonuses (1 bonus = 1 burle) to reduce the payment. She can cover at most half of the payment using bonuses. However, 1 bonus will be added to the customer's bonus balance per each 10 burles she paid.

Formally:
a customer can choose any number x of bonuses to use (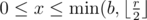)), the customer's bonus balance is reduced by x, the customer pays r-x burles, the customer's bonus balance is increased by ⌊(r-x)/10⌋ (i.e. integer division rounded down is used).
Initially, there are b bonuses on Polycarp's account. Polycarp is going to have a lunch in "Ber Patio" for the next n days. He estimated the values a1,a2,...,an, where ai is the number of burles in a receipt for the i-th day. The sum over all receipts doesn't exceed 105 burles.

Write a program to find the minimum number of burles Polycarp has to spend and an optimal strategy to use bonuses.

The first line contains two integer numbers n and b (1 \le n \le 5000, 0 \le b \le 105) - number of days and initial number of bonuses Polycarp has.

The second line contains the integer sequence a1,a2,...,an (1 \le ai \le 1000), where ai is the amount of burles in the i-th day's receipt.

It is guaranteed that the sum of all receipts does not exceed 105 burles.

On the first line, print the expected minimal number of burles to pay for all n receipts.

On the second line, print the sequence of integer numbers b1,b2,...,bn, where bi is the number of bonuses to use on the i-th day. If there are multiple solutions, print any of them.