Mike wants to prepare for IMO but he doesn't know geometry, so his teacher gave him an interesting geometry problem. Let's define f([l,r])=r-l+1 to be the number of integer points in the segment [l,r] with l \le r (say that 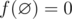). You are given two integers n and k and n closed intervals [li,ri] on OX axis and you have to find: In other words, you should find the sum of the number of integer points in the intersection of any k of the segments. As the answer may be very large, output it modulo 1000000007 (109+7).Mike can't solve this problem so he needs your help. You will help him, won't you?

Input The first line contains two integers n and k (1 \le k \le n \le 200000)- the number of segments and the number of segments in intersection groups respectively.Then n lines follow, the i-th line contains two integers li,ri (-109 \le li \le ri \le 109), describing i-th segment bounds.

Output Print one integer number- the answer to Mike's problem modulo 1000000007 (109+7) in the only line.

In the first example: ;;.So the answer is 2+1+2=5.