2417.Bear and Two Paths
Time Limit: 1s Memory Limit: 256MBBearland has n cities, numbered 1 through n. Cities are connected via bidirectional roads. Each road connects two distinct cities. No two roads connect the same pair of cities.Bear Limak was once in a city a and he wanted to go to a city b. There was no direct connection so he decided to take a long walk, visiting each city exactly once. Formally: There is no road between a and b. There exists a sequence (path) of n distinct cities v1,v2,...,vn that v1=a, vn=b and there is a road between vi and vi+1 for  . On the other day, the similar thing happened. Limak wanted to travel between a city c and a city d. There is no road between them but there exists a sequence of n distinct cities u1,u2,...,un that u1=c, un=d and there is a road between ui and ui+1 for
. On the other day, the similar thing happened. Limak wanted to travel between a city c and a city d. There is no road between them but there exists a sequence of n distinct cities u1,u2,...,un that u1=c, un=d and there is a road between ui and ui+1 for  .Also, Limak thinks that there are at most k roads in Bearland. He wonders whether he remembers everything correctly.Given n, k and four distinct cities a, b, c, d, can you find possible paths (v1,...,vn) and (u1,...,un) to satisfy all the given conditions? Find any solution or print -1 if it's impossible.
.Also, Limak thinks that there are at most k roads in Bearland. He wonders whether he remembers everything correctly.Given n, k and four distinct cities a, b, c, d, can you find possible paths (v1,...,vn) and (u1,...,un) to satisfy all the given conditions? Find any solution or print -1 if it's impossible.
Input Format(From the terminal/stdin)
Input The first line of the input contains two integers n and k (4 \le n \le 1000, n-1 \le k \le 2n-2)- the number of cities and the maximum allowed number of roads, respectively.The second line contains four distinct integers a, b, c and d (1 \le a,b,c,d \le n).
Output Format(To the terminal/stdout)
Output Print -1 if it's impossible to satisfy all the given conditions. Otherwise, print two lines with paths descriptions. The first of these two lines should contain n distinct integers v1,v2,...,vn where v1=a and vn=b. The second line should contain n distinct integers u1,u2,...,un where u1=c and un=d.Two paths generate at most 2n-2 roads: (v1,v2),(v2,v3),...,(vn-1,vn),(u1,u2),(u2,u3),...,(un-1,un). Your answer will be considered wrong if contains more than k distinct roads or any other condition breaks. Note that (x,y) and (y,x) are the same road.
Sample Input 1
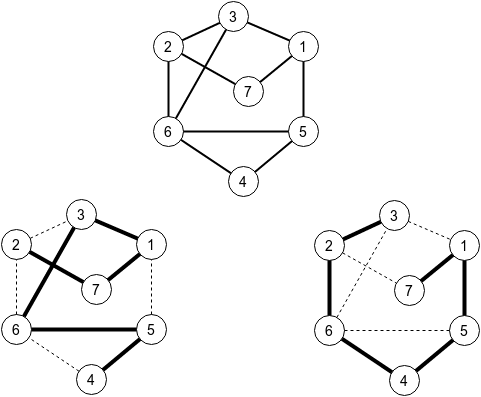
7 11 2 4 7 3· \n · · · \n
Sample Output 1
2 7 1 3 6 5 4 7 1 5 4 6 2 3· · · · · · \n · · · · · · \n
Hints
In the first sample test, there should be 7 cities and at most 11 roads. The provided sample solution generates 10 roads, as in the drawing. You can also see a simple path of length n between 2 and 4, and a path between 7 and 3.