Limak is a little polar bear. He doesn't have many toys and thus he often plays with polynomials.

He considers a polynomial valid if its degree is n and its coefficients are integers not exceeding k by the absolute value. More formally:

Let a0,a1,...,an denote the coefficients, so 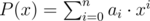. Then, a polynomial P(x) is valid if all the following conditions are satisfied:
ai is integer for every i; |ai| \le k for every i; an \neq 0.
Limak has recently got a valid polynomial P with coefficients a0,a1,a2,...,an. He noticed that P(2) \neq 0 and he wants to change it. He is going to change one coefficient to get a valid polynomial Q of degree n that Q(2)=0. Count the number of ways to do so. You should count two ways as a distinct if coefficients of target polynoms differ.

The first line contains two integers n and k (1 \le n \le 200000,1 \le k \le 109)- the degree of the polynomial and the limit for absolute values of coefficients.

The second line contains n+1 integers a0,a1,...,an (|ai| \le k,an \neq 0)- describing a valid polynomial 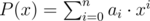. It's guaranteed that P(2) \neq 0.

Print the number of ways to change one coefficient to get a valid polynomial Q that Q(2)=0.

In the first sample, we are given a polynomial P(x)=10-9x-3x2+5x3.

Limak can change one coefficient in three ways:
He can set a0=-10. Then he would get Q(x)=-10-9x-3x2+5x3 and indeed Q(2)=-10-18-12+40=0. Or he can set a2=-8. Then Q(x)=10-9x-8x2+5x3 and indeed Q(2)=10-18-32+40=0. Or he can set a1=-19. Then Q(x)=10-19x-3x2+5x3 and indeed Q(2)=10-38-12+40=0.
In the second sample, we are given the same polynomial. This time though, k is equal to 12 instead of 109. Two first of ways listed above are still valid but in the third way we would get |a1| \gt k what is not allowed. Thus, the answer is 2 this time.