The semester is already ending, so Danil made an effort and decided to visit a lesson on harmony analysis to know how does the professor look like, at least. Danil was very bored on this lesson until the teacher gave the group a simple task: find 4 vectors in 4-dimensional space, such that every coordinate of every vector is 1 or -1 and any two vectors are orthogonal. Just as a reminder, two vectors in n-dimensional space are considered to be orthogonal if and only if their scalar product is equal to zero, that is: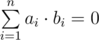
.
Danil quickly managed to come up with the solution for this problem and the teacher noticed that the problem can be solved in a more general case for 2k vectors in 2k-dimensinoal space. When Danil came home, he quickly came up with the solution for this problem. Can you cope with it?

The only line of the input contains a single integer k (0 \le k \le 9).

Print 2k lines consisting of 2k characters each. The j-th character of the i-th line must be equal to '*' if the j-th coordinate of the i-th vector is equal to -1, and must be equal to '+' if it's equal to +1. It's guaranteed that the answer always exists.

If there are many correct answers, print any.

Consider all scalar products in example:
Vectors 1 and 2: (+1) \cdot (+1)+(+1) \cdot (-1)+(-1) \cdot (+1)+(-1) \cdot (-1)=0 Vectors 1 and 3: (+1) \cdot (+1)+(+1) \cdot (+1)+(-1) \cdot (+1)+(-1) \cdot (+1)=0 Vectors 1 and 4: (+1) \cdot (+1)+(+1) \cdot (-1)+(-1) \cdot (-1)+(-1) \cdot (+1)=0 Vectors 2 and 3: (+1) \cdot (+1)+(-1) \cdot (+1)+(+1) \cdot (+1)+(-1) \cdot (+1)=0 Vectors 2 and 4: (+1) \cdot (+1)+(-1) \cdot (-1)+(+1) \cdot (-1)+(-1) \cdot (+1)=0 Vectors 3 and 4: (+1) \cdot (+1)+(+1) \cdot (-1)+(+1) \cdot (-1)+(+1) \cdot (+1)=0