Genos needs your help. He was asked to solve the following programming problem by Saitama:

The length of some string s is denoted |s|. The Hamming distance between two strings s and t of equal length is defined as 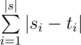, where si is the i-th character of s and ti is the i-th character of t. For example, the Hamming distance between string "0011" and string "0110" is |0-0|+|0-1|+|1-1|+|1-0|=0+1+0+1=2.

Given two binary strings a and b, find the sum of the Hamming distances between a and all contiguous substrings of b of length |a|.

The first line of the input contains binary string a (1 \le |a| \le 200000).

The second line of the input contains binary string b (|a| \le |b| \le 200000).

Both strings are guaranteed to consist of characters '0' and '1' only.

Print a single integer- the sum of Hamming distances between a and all contiguous substrings of b of length |a|.

For the first sample case, there are four contiguous substrings of b of length |a|: "00", "01", "11", and "11". The distance between "01" and "00" is |0-0|+|1-0|=1. The distance between "01" and "01" is |0-0|+|1-1|=0. The distance between "01" and "11" is |0-1|+|1-1|=1. Last distance counts twice, as there are two occurrences of string "11". The sum of these edit distances is 1+0+1+1=3.

The second sample case is described in the statement.