After seeing the "ALL YOUR BASE ARE BELONG TO US" meme for the first time, numbers X and Y realised that they have different bases, which complicated their relations.

You're given a number X represented in base bx and a number Y represented in base by. Compare those two numbers.

The first line of the input contains two space-separated integers n and bx (1 \le n \le 10, 2 \le bx \le 40), where n is the number of digits in the bx-based representation of X.

The second line contains n space-separated integers x1,x2,...,xn (0 \le xi \lt bx) - the digits of X. They are given in the order from the most significant digit to the least significant one.

The following two lines describe Y in the same way: the third line contains two space-separated integers m and by (1 \le m \le 10, 2 \le by \le 40, bx \neq by), where m is the number of digits in the by-based representation of Y, and the fourth line contains m space-separated integers y1,y2,...,ym (0 \le yi \lt by) - the digits of Y.

There will be no leading zeroes. Both X and Y will be positive. All digits of both numbers are given in the standard decimal numeral system.

Output a single character (quotes for clarity):
' \lt ' if X \lt Y ' \gt ' if X \gt Y '=' if X=Y

In the first sample, X=1011112=4710=Y.

In the second sample, X=1023=215 and Y=245=1123, thus X \lt Y.

In the third sample, 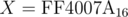and Y=48031509. We may notice that X starts with much larger digits and bx is much larger than by, so X is clearly larger than Y.