2585.Acyclic Organic Compounds
Time Limit: 1s Memory Limit: 256MBYou are given a tree T with n vertices (numbered 1 through n) and a letter in each vertex. The tree is rooted at vertex 1.Let's look at the subtree Tv of some vertex v. It is possible to read a string along each simple path starting at v and ending at some vertex in Tv (possibly v itself). Let's denote the number of distinct strings which can be read this way as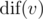 
. Also, there's a number cv assigned to each vertex v. We are interested in vertices with the maximum value of 
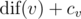.You should compute two statistics: the maximum value of 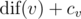and the number of vertices v with the maximum .
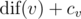Input Format(From the terminal/stdin)
Input The first line of the input contains one integer n (1 \le n \le 300000)- the number of vertices of the tree.The second line contains n space-separated integers ci (0 \le ci \le 109).The third line contains a string s consisting of n lowercase English letters- the i-th character of this string is the letter in vertex i.The following n-1 lines describe the tree T. Each of them contains two space-separated integers u and v (1 \le u,v \le n) indicating an edge between vertices u and v.It's guaranteed that the input will describe a tree.
Output Format(To the terminal/stdout)
Output Print two lines. On the first line, print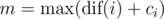 
over all 1 \le i \le n. On the second line, print the number of vertices v for which 
.
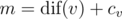Sample Input 1
10 1 2 7 20 20 30 40 50 50 50 cacabbcddd 1 2 6 8 7 2 6 2 5 4 5 9 3 10 2 5 2 3\n · · · · · · · · · \n \n · \n · \n · \n · \n · \n · \n · \n · \n · \n
Sample Output 1
51 3\n \n
Sample Input 2
6 0 2 4 1 1 1 raaaba 1 2 2 3 2 4 2 5 3 6\n · · · · · \n \n · \n · \n · \n · \n · \n
Sample Output 2
6 2\n \n
Hints
In the first sample, the tree looks like this: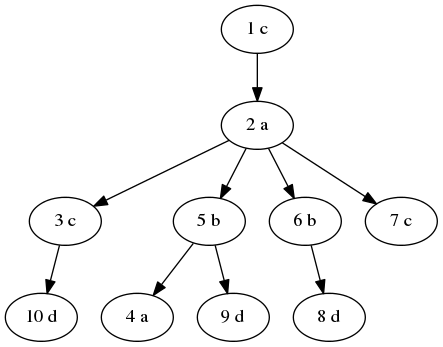 
The sets of strings that can be read from individual vertices are: 
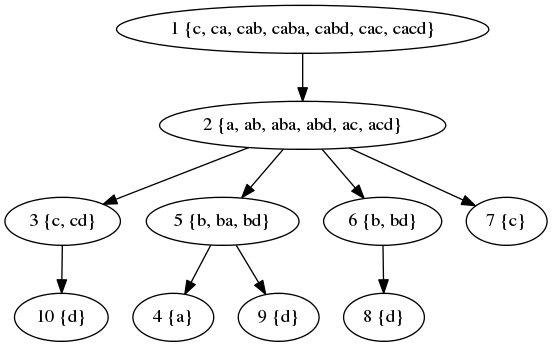Finally, the values of 
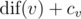are: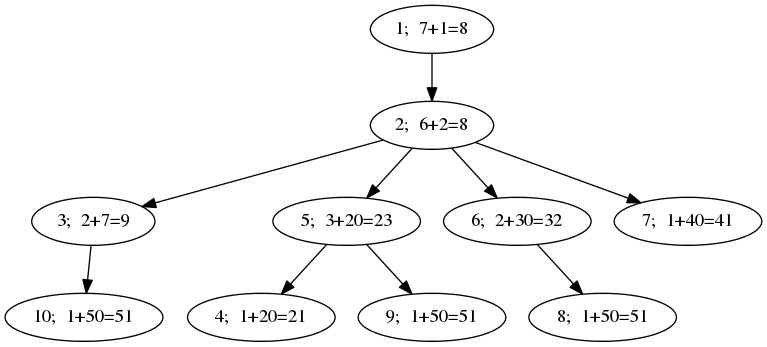 
In the second sample, the values of 
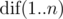are (5,4,2,1,1,1). The distinct strings read in T2 are 
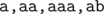; note that 
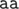can be read down to vertices 3 or 4.