2618.REQ
Time Limit: 1s Memory Limit: 256MBToday on a math lesson the teacher told Vovochka that the Euler function of a positive integer φ(n) is an arithmetic function that counts the positive integers less than or equal to n that are relatively prime to n. The number 1 is coprime to all the positive integers and φ(1)=1.
Now the teacher gave Vovochka an array of n positive integers a1,a2,...,an and a task to process q queries li ri- to calculate and print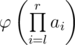 
modulo 109+7. As it is too hard for a second grade school student, you've decided to help Vovochka.
Input Format(From the terminal/stdin)
The first line of the input contains number n (1 \le n \le 200000)- the length of the array given to Vovochka. The second line contains n integers a1,a2,...,an (1 \le ai \le 106).
The third line contains integer q (1 \le q \le 200000)- the number of queries. Next q lines contain the queries, one per line. Each query is defined by the boundaries of the segment li and ri (1 \le li \le ri \le n).
Output Format(To the terminal/stdout)
Print q numbers - the value of the Euler function for each query, calculated modulo 109+7.
Sample Input 1
10 1 2 3 4 5 6 7 8 9 10 7 1 1 3 8 5 6 4 8 8 10 7 9 7 10\n · · · · · · · · · \n \n · \n · \n · \n · \n · \n · \n · \n
Sample Output 1
1 4608 8 1536 192 144 1152\n \n \n \n \n \n \n
Sample Input 2
7 24 63 13 52 6 10 1 6 3 5 4 7 1 7 2 4 3 6 2 6\n · · · · · · \n \n · \n · \n · \n · \n · \n · \n
Sample Output 2
1248 768 12939264 11232 9984 539136\n \n \n \n \n \n
Hints
In the second sample the values are calculated like that:
φ(13 \cdot 52 \cdot 6)=φ(4056)=1248 φ(52 \cdot 6 \cdot 10 \cdot 1)=φ(3120)=768 φ(24 \cdot 63 \cdot 13 \cdot 52 \cdot 6 \cdot 10 \cdot 1)=φ(61326720)=12939264 φ(63 \cdot 13 \cdot 52)=φ(42588)=11232 φ(13 \cdot 52 \cdot 6 \cdot 10)=φ(40560)=9984 φ(63 \cdot 13 \cdot 52 \cdot 6 \cdot 10)=φ(2555280)=539136