Recently Duff has been a soldier in the army. Malek is her commander.Their country, Andarz Gu has n cities (numbered from 1 to n) and n-1 bidirectional roads. Each road connects two different cities. There exist a unique path between any two cities.There are also m people living in Andarz Gu (numbered from 1 to m). Each person has and ID number. ID number of i-th person is i and he/she lives in city number ci. Note that there may be more than one person in a city, also there may be no people living in the city. Malek loves to order. That's why he asks Duff to answer to q queries. In each query, he gives her numbers v,u and a.To answer a query:Assume there are x people living in the cities lying on the path from city v to city u. Assume these people's IDs are p1,p2,...,px in increasing order. If k=min(x,a), then Duff should tell Malek numbers k,p1,p2,...,pk in this order. In the other words, Malek wants to know a minimums on that path (or less, if there are less than a people).Duff is very busy at the moment, so she asked you to help her and answer the queries.

Input The first line of input contains three integers, n,m and q (1 \le n,m,q \le 105).The next n-1 lines contain the roads. Each line contains two integers v and u, endpoints of a road (1 \le v,u \le n, v \neq u).Next line contains m integers c1,c2,...,cm separated by spaces (1 \le ci \le n for each 1 \le i \le m).Next q lines contain the queries. Each of them contains three integers, v,u and a (1 \le v,u \le n and 1 \le a \le 10).

Output For each query, print numbers k,p1,p2,...,pk separated by spaces in one line.

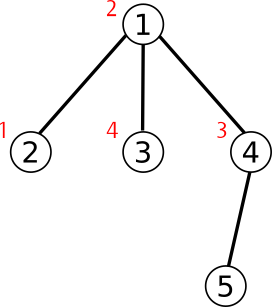
Graph of Andarz Gu in the sample case is as follows (ID of people in each city are written next to them):