While Duff was resting in the beach, she accidentally found a strange array b0,b1,...,bl-1 consisting of l positive integers. This array was strange because it was extremely long, but there was another (maybe shorter) array, a0,...,an-1 that b can be build from a with formula: bi=ai mod n where a mod b denoted the remainder of dividing a by b. Duff is so curious, she wants to know the number of subsequences of b like bi1,bi2,...,bix (0 \le i1 \lt i2 \lt ... \lt ix \lt l), such that: 1 \le x \le k For each 1 \le j \le x-1, 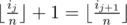For each 1 \le j \le x-1, bij \le bij+1. i.e this subsequence is non-decreasing. Since this number can be very large, she want to know it modulo 109+7.Duff is not a programmer, and Malek is unavailable at the moment. So she asked for your help. Please tell her this number.

Input The first line of input contains three integers, n,l and k (1 \le n,k, n \times k \le 106 and 1 \le l \le 1018).The second line contains n space separated integers, a0,a1,...,an-1 (1 \le ai \le 109 for each 0 \le i \le n-1).

Output Print the answer modulo 1000000007 in one line.

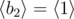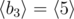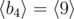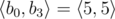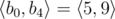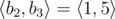In the first sample case, . So all such sequences are: , , , , , , , , and .