On a plane are n points (xi, yi) with integer coordinates between 0 and 106. The distance between the two points with numbers a and b is said to be the following value: 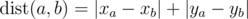(the distance calculated by such formula is called Manhattan distance).We call a hamiltonian path to be some permutation pi of numbers from 1 to n. We say that the length of this path is value 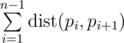.Find some hamiltonian path with a length of no more than 25 \times 108. Note that you do not have to minimize the path length.

Input The first line contains integer n (1 \le n \le 106).The i+1-th line contains the coordinates of the i-th point: xi and yi (0 \le xi,yi \le 106).It is guaranteed that no two points coincide.

Output Print the permutation of numbers pi from 1 to n - the sought Hamiltonian path. The permutation must meet the inequality 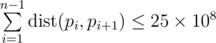.If there are multiple possible answers, print any of them.It is guaranteed that the answer exists.

In the sample test the total distance is: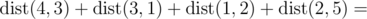(|5-3|+|0-4|)+(|3-0|+|4-7|)+(|0-8|+|7-10|)+(|8-9|+|10-12|)=2+4+3+3+8+3+1+2=26