Some time ago Leonid have known about idempotent functions. Idempotent function defined on a set {1,2,...,n} is such function 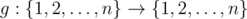, that for any 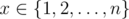the formula g(g(x))=g(x) holds.Let's denote as f(k)(x) the function f applied k times to the value x. More formally, f(1)(x)=f(x), f(k)(x)=f(f(k-1)(x)) for each k \gt 1.You are given some function 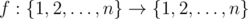. Your task is to find minimum positive integer k such that function f(k)(x) is idempotent.

Input In the first line of the input there is a single integer n (1 \le n \le 200) - the size of function f domain.In the second line follow f(1),f(2),...,f(n) (1 \le f(i) \le n for each 1 \le i \le n), the values of a function.

Output Output minimum k such that function f(k)(x) is idempotent.

In the first sample test function f(x)=f(1)(x) is already idempotent since f(f(1))=f(1)=1, f(f(2))=f(2)=2, f(f(3))=f(3)=2, f(f(4))=f(4)=4.In the second sample test: function f(x)=f(1)(x) isn't idempotent because f(f(1))=3 but f(1)=2; function f(x)=f(2)(x) is idempotent since for any x it is true that f(2)(x)=3, so it is also true that f(2)(f(2)(x))=3. In the third sample test: function f(x)=f(1)(x) isn't idempotent because f(f(1))=3 but f(1)=2; function f(f(x))=f(2)(x) isn't idempotent because f(2)(f(2)(1))=2 but f(2)(1)=3; function f(f(f(x)))=f(3)(x) is idempotent since it is identity function: f(3)(x)=x for any 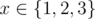meaning that the formula f(3)(f(3)(x))=f(3)(x) also holds.