Tavas lives in Tavaspolis. Tavaspolis has n cities numbered from 1 to n connected by n-1 bidirectional roads. There exists a path between any two cities. Also each road has a length. Tavas' favorite strings are binary strings (they contain only 0 and 1). For any binary string like s=s1s2... sk, T(s) is its Goodness. T(s) can be calculated as follows:Consider there are exactly m blocks of 1s in this string (a block of 1s in s is a maximal consecutive substring of s that only contains 1) with lengths x1,x2,...,xm.Define 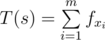where f is a given sequence (if m=0, then T(s)=0).Tavas loves queries. He asks you to answer q queries. In each query he gives you numbers v,u,l and you should print following number:Consider the roads on the path from city v to city u: e1,e2,...,ex.Build the binary string b of length x such that: bi=1 if and only if l \le w(ei) where w(e) is the length of road e.You should print T(b) for this query.

Input The first line of input contains integers n and q (2 \le n \le 105 and 1 \le q \le 105).The next line contains n-1 space separated integers f1,f2,...,fn-1 (|fi| \le 1000).The next n-1 lines contain the details of the roads. Each line contains integers v,u and w and it means that there's a road between cities v and u of length w (1 \le v,u \le n and 1 \le w \le 109).The next q lines contain the details of the queries. Each line contains integers v,u,l (1 \le v,u \le n, v \neq u and 1 \le l \le 109).

Output Print the answer of each query in a single line.