Let's define the sum of two permutations p and q of numbers 0,1,...,(n-1) as permutation 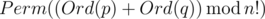, where Perm(x) is the x-th lexicographically permutation of numbers 0,1,...,(n-1) (counting from zero), and Ord(p) is the number of permutation p in the lexicographical order.For example, Perm(0)=(0,1,...,n-2,n-1), Perm(n!-1)=(n-1,n-2,...,1,0)Misha has two permutations, p and q. Your task is to find their sum.Permutation a=(a0,a1,...,an-1) is called to be lexicographically smaller than permutation b=(b0,b1,...,bn-1), if for some k following conditions hold: a0=b0,a1=b1,...,ak-1=bk-1,ak \lt bk.

Input The first line contains an integer n (1 \le n \le 200000).The second line contains n distinct integers from 0 to n-1, separated by a space, forming permutation p.The third line contains n distinct integers from 0 to n-1, separated by spaces, forming permutation q.

Output Print n distinct integers from 0 to n-1, forming the sum of the given permutations. Separate the numbers by spaces.

Permutations of numbers from 0 to 1 in the lexicographical order: (0,1),(1,0).In the first sample Ord(p)=0 and Ord(q)=0, so the answer is 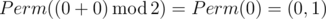.In the second sample Ord(p)=0 and Ord(q)=1, so the answer is 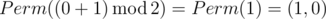.Permutations of numbers from 0 to 2 in the lexicographical order: (0,1,2),(0,2,1),(1,0,2),(1,2,0),(2,0,1),(2,1,0).In the third sample Ord(p)=3 and Ord(q)=5, so the answer is .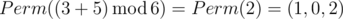