As you know, an undirected connected graph with n nodes and n-1 edges is called a tree. You are given an integer d and a tree consisting of n nodes. Each node i has a value ai associated with it.

We call a set S of tree nodes valid if following conditions are satisfied:
S is non-empty. S is connected. In other words, if nodes u and v are in S, then all nodes lying on the simple path between u and v should also be presented in S. .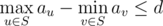
Your task is to count the number of valid sets. Since the result can be very large, you must print its remainder modulo 1000000007 (109+7).

The first line contains two space-separated integers d (0 \le d \le 2000) and n (1 \le n \le 2000).

The second line contains n space-separated positive integers a1,a2,...,an(1 \le ai \le 2000).

Then the next n-1 line each contain pair of integers u and v (1 \le u,v \le n) denoting that there is an edge between u and v. It is guaranteed that these edges form a tree.

Print the number of valid sets modulo 1000000007.

In the first sample, there are exactly 8 valid sets: {1},{2},{3},{4},{1,2},{1,3},{3,4} and {1,3,4}. Set {1,2,3,4} is not valid, because the third condition isn't satisfied. Set {1,4} satisfies the third condition, but conflicts with the second condition.