Imagine a city with n junctions and m streets. Junctions are numbered from 1 to n.

In order to increase the traffic flow, mayor of the city has decided to make each street one-way. This means in the street between junctions u and v, the traffic moves only from u to v or only from v to u.

The problem is to direct the traffic flow of streets in a way that maximizes the number of pairs (u,v) where 1 \le u,v \le n and it is possible to reach junction v from u by passing the streets in their specified direction. Your task is to find out maximal possible number of such pairs.

The first line of input contains integers n and m, (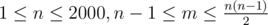), denoting the number of junctions and streets of the city.

Each of the following m lines contains two integers u and v, (u \neq v), denoting endpoints of a street in the city.

Between every two junctions there will be at most one street. It is guaranteed that before mayor decision (when all streets were two-way) it was possible to reach each junction from any other junction.

Print the maximal number of pairs (u,v) such that that it is possible to reach junction v from u after directing the streets.

In the first sample, if the mayor makes first and second streets one-way towards the junction 1 and third and fourth streets in opposite direction, there would be 13 pairs of reachable junctions: {(1,1),(2,2),(3,3),(4,4),(5,5),(2,1),(3,1),(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)}