3142.DZY Loves Fibonacci Numbers
Time Limit: 1s Memory Limit: 256MBIn mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
F1=1;F2=1;Fn=Fn-1+Fn-2(n \gt 2).
DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of n integers: a1,a2,...,an. Moreover, there are m queries, each query has one of the two types:
Format of the query "1 l r". In reply to the query, you need to add Fi-l+1 to each element ai, where l \le i \le r. Format of the query "2 l r". In reply to the query you should output the value of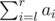 
modulo 1000000009(109+9).
Help DZY reply to all the queries.
Input Format(From the terminal/stdin)
The first line of the input contains two integers n and m (1 \le n,m \le 300000). The second line contains n integers a1,a2,...,an(1 \le ai \le 109) - initial array a.
Then, m lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1 \le l \le r \le n holds.
Output Format(To the terminal/stdout)
For each query of the second type, print the value of the sum on a single line.
Sample Input
4 4 1 2 3 4 1 1 4 2 1 4 1 2 4 2 1 3· \n · · · \n · · \n · · \n · · \n · · \n
Sample Output
17 12\n \n
Hints
After the first query, a=[2,3,5,7].
For the second query, sum=2+3+5+7=17.
After the third query, a=[2,4,6,9].
For the fourth query, sum=2+4+6=12.