3147.DZY Loves Planting
Time Limit: 1s Memory Limit: 256MBDZY loves planting, and he enjoys solving tree problems.
DZY has a weighted tree (connected undirected graph without cycles) containing n nodes (they are numbered from 1 to n). He defines the function g(x,y) (1 \le x,y \le n) as the longest edge in the shortest path between nodes x and y. Specially g(z,z)=0 for every z.
For every integer sequence p1,p2,...,pn (1 \le pi \le n), DZY defines f(p) as 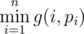 .
.
DZY wants to find such a sequence p that f(p) has maximum possible value. But there is one more restriction: the element j can appear in p at most xj times.
Please, find the maximum possible f(p) under the described restrictions.
Input Format(From the terminal/stdin)
The first line contains an integer n(1 \le n \le 3000).
Each of the next n-1 lines contains three integers ai,bi,ci(1 \le ai,bi \le n;1 \le ci \le 10000), denoting an edge between ai and bi with length ci. It is guaranteed that these edges form a tree.
Each of the next n lines describes an element of sequence x. The j-th line contains an integer xj(1 \le xj \le n).
Output Format(To the terminal/stdout)
Print a single integer representing the answer.
Sample Input 1
4 1 2 1 2 3 2 3 4 3 1 1 1 1\n · · \n · · \n · · \n \n \n \n \n
Sample Output 1
2\n
Sample Input 2
4 1 2 1 2 3 2 3 4 3 4 4 4 4\n · · \n · · \n · · \n \n \n \n \n
Sample Output 2
3\n
Hints
In the first sample, one of the optimal p is [4,3,2,1].