3150.DZY Loves Physics
Time Limit: 1s Memory Limit: 256MBDZY loves Physics, and he enjoys calculating density.Almost everything has density, even a graph. We define the density of a non-directed graph (nodes and edges of the graph have some values) as follows: 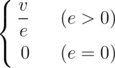 where v is the sum of the values of the nodes, e is the sum of the values of the edges.
where v is the sum of the values of the nodes, e is the sum of the values of the edges.
Once DZY got a graph G, now he wants to find a connected induced subgraph G' of the graph, such that the density of G' is as large as possible.An induced subgraph G'(V',E') of a graph G(V,E) is a graph that satisfies: 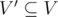 ; edge
; edge 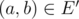 if and only if
if and only if 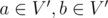 , and edge
, and edge 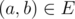 ; the value of an edge in G' is the same as the value of the corresponding edge in G, so as the value of a node. Help DZY to find the induced subgraph with maximum density. Note that the induced subgraph you choose must be connected.
; the value of an edge in G' is the same as the value of the corresponding edge in G, so as the value of a node. Help DZY to find the induced subgraph with maximum density. Note that the induced subgraph you choose must be connected. 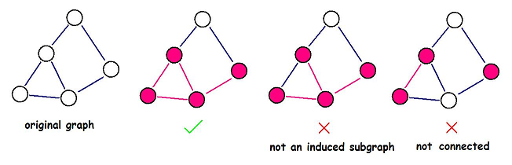
Input Format(From the terminal/stdin)
Input The first line contains two space-separated integers n(1 \le n \le 500),  . Integer n represents the number of nodes of the graph G, m represents the number of edges.The second line contains n space-separated integers xi(1 \le xi \le 106), where xi represents the value of the i-th node. Consider the graph nodes are numbered from 1 to n.Each of the next m lines contains three space-separated integers ai,bi,ci(1 \le ai \lt bi \le n;1 \le ci \le 103), denoting an edge between node ai and bi with value ci. The graph won't contain multiple edges.
. Integer n represents the number of nodes of the graph G, m represents the number of edges.The second line contains n space-separated integers xi(1 \le xi \le 106), where xi represents the value of the i-th node. Consider the graph nodes are numbered from 1 to n.Each of the next m lines contains three space-separated integers ai,bi,ci(1 \le ai \lt bi \le n;1 \le ci \le 103), denoting an edge between node ai and bi with value ci. The graph won't contain multiple edges.
Output Format(To the terminal/stdout)
Output Output a real number denoting the answer, with an absolute or relative error of at most 10-9.
Sample Input 3
5 6 13 56 73 98 17 1 2 56 1 3 29 1 4 42 2 3 95 2 4 88 3 4 63· \n · · · · \n · · \n · · \n · · \n · · \n · · \n · · \n
Sample Output 3
2.965517241379311\n
Hints
In the first sample, you can only choose an empty subgraph, or the subgraph containing only node 1.In the second sample, choosing the whole graph is optimal.