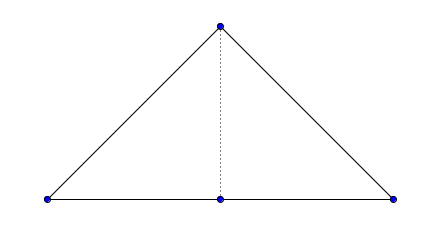
3171.The Child and Polygon
Time Limit: 1s Memory Limit: 256MBThis time our child has a simple polygon. He has to find the number of ways to split the polygon into non-degenerate triangles, each way must satisfy the following requirements: each vertex of each triangle is one of the polygon vertex; each side of the polygon must be the side of exactly one triangle; the area of intersection of every two triangles equals to zero, and the sum of all areas of triangles equals to the area of the polygon; each triangle must be completely inside the polygon; each side of each triangle must contain exactly two vertices of the polygon. The picture below depicts an example of a correct splitting.  Please, help the child. Calculate the described number of ways modulo 1000000007 (109+7) for him.
Please, help the child. Calculate the described number of ways modulo 1000000007 (109+7) for him.
Input Format(From the terminal/stdin)
Input The first line contains one integer n (3 \le n \le 200) - the number of vertices of the polygon. Then follow n lines, each line containing two integers. The i-th line contains xi,yi (|xi|,|yi| \le 107) - the i-th vertex of the polygon in clockwise or counterclockwise order.It's guaranteed that the polygon is simple.
Output Format(To the terminal/stdout)
Output Output the number of ways modulo 1000000007 (109+7).
Hints
In the first sample, there are two possible splittings: 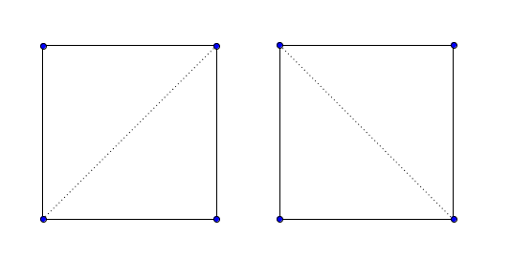 In the second sample, there are only one possible splitting:
In the second sample, there are only one possible splitting: