3277.Strictly Positive Matrix
Time Limit: 1s Memory Limit: 256MBYou have matrix a of size n \times n. Let's number the rows of the matrix from 1 to n from top to bottom, let's number the columns from 1 to n from left to right. Let's use aij to represent the element on the intersection of the i-th row and the j-th column.
Matrix a meets the following two conditions:
for any numbers i,j (1 \le i,j \le n) the following inequality holds: aij \ge 0; 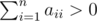 .
.
Matrix b is strictly positive, if for any numbers i,j (1 \le i,j \le n) the inequality bij \gt 0 holds. You task is to determine if there is such integer k \ge 1, that matrix ak is strictly positive.
Input Format(From the terminal/stdin)
The first line contains integer n (2 \le n \le 2000) - the number of rows and columns in matrix a.
The next n lines contain the description of the rows of matrix a. The i-th line contains n non-negative integers ai1,ai2,...,ain (0 \le aij \le 50). It is guaranteed that 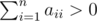 .
.
Output Format(To the terminal/stdout)
If there is a positive integer k \ge 1, such that matrix ak is strictly positive, print "YES" (without the quotes). Otherwise, print "NO" (without the quotes).