Bike is interested in permutations. A permutation of length n is an integer sequence such that each integer from 0 to (n-1) appears exactly once in it. For example, [0,2,1] is a permutation of length 3 while both [0,2,2] and [1,2,3] is not.A permutation triple of permutations of length n (a,b,c) is called a Lucky Permutation Triple if and only if . The sign ai denotes the i-th element of permutation a. The modular equality described above denotes that the remainders after dividing ai+bi by n and dividing ci by n are equal.Now, he has an integer n and wants to find a Lucky Permutation Triple. Could you please help him?

Input The first line contains a single integer n (1 \le n \le 105).

Output If no Lucky Permutation Triple of length n exists print -1.Otherwise, you need to print three lines. Each line contains n space-seperated integers. The first line must contain permutation a, the second line - permutation b, the third - permutation c.If there are multiple solutions, print any of them.

In Sample 1, the permutation triple ([1,4,3,2,0],[1,0,2,4,3],[2,4,0,1,3]) is Lucky Permutation Triple, as following hold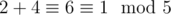s: ; ; ; ; . In Sample 2, you can easily notice that no lucky permutation triple exists.