John Doe has found the beautiful permutation formula.

Let's take permutation p=p1,p2,...,pn. Let's define transformation f of this permutation:

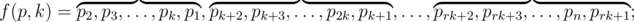
where k (k \gt 1) is an integer, the transformation parameter, r is such maximum integer that rk \le n. If rk=n, then elements prk+1,prk+2 and so on are omitted. In other words, the described transformation of permutation p cyclically shifts to the left each consecutive block of length k and the last block with the length equal to the remainder after dividing n by k.

John Doe thinks that permutation f(f(...f(p=[1,2,...,n],2)...,n-1),n) is beautiful. Unfortunately, he cannot quickly find the beautiful permutation he's interested in. That's why he asked you to help him.

Your task is to find a beautiful permutation for the given n. For clarifications, see the notes to the third sample.

A single line contains integer n (2 \le n \le 106).

Print n distinct space-separated integers from 1 to n - a beautiful permutation of size n.

A note to the third test sample:
f([1,2,3,4],2)=[2,1,4,3] f([2,1,4,3],3)=[1,4,2,3] f([1,4,2,3],4)=[4,2,3,1]