You've got a non-decreasing sequence x1,x2,...,xn (1 \le x1 \le x2 \le ... \le xn \le q). You've also got two integers a and b (a \le b;a \cdot (n-1) \lt q).

Your task is to transform sequence x1,x2,...,xn into some sequence y1,y2,...,yn (1 \le yi \le q;a \le yi+1-yi \le b). The transformation price is the following sum: 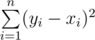. Your task is to choose such sequence y that minimizes the described transformation price.

The first line contains four integers n,q,a,b (2 \le n \le 6000;1 \le q,a,b \le 109;a \cdot (n-1) \lt q;a \le b).

The second line contains a non-decreasing integer sequence x1,x2,...,xn (1 \le x1 \le x2 \le ... \le xn \le q).

In the first line print n real numbers - the sought sequence y1,y2,...,yn (1 \le yi \le q;a \le yi+1-yi \le b). In the second line print the minimum transformation price, that is, .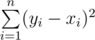

If there are multiple optimal answers you can print any of them.

The answer will be considered correct if the absolute or relative error doesn't exceed 10-6.