You are given the following points with integer coordinates on the plane: M0,A0,A1,...,An-1, where n is odd number. Now we define the following infinite sequence of points Mi: Mi is symmetric to Mi-1 according 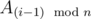(for every natural number i). Here point B is symmetric to A according M, if M is the center of the line segment AB. Given index j find the point Mj.

On the first line you will be given an integer n (1 \le n \le 105), which will be odd, and j (1 \le j \le 1018), where j is the index of the desired point. The next line contains two space separated integers, the coordinates of M0. After that n lines follow, where the i-th line contain the space separated integer coordinates of the point Ai-1. The absolute values of all input coordinates will not be greater then 1000.

On a single line output the coordinates of Mj, space separated.