3833 - Number Challenge - PK@Contest.bjtu

3833.Number Challenge

Time Limit: 1s Memory Limit: 256MB

Let's denote d(n) as the number of divisors of a positive integer n. You are given three integers a, b and c. Your task is to calculate the following sum:

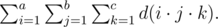
$3833_1.png$

Find the sum modulo 1073741824 (230).

Input Format(From the terminal/stdin)

The first line contains three space-separated integers a, b and c (1 \le a,b,c \le 2000).

Output Format(To the terminal/stdout)

Print a single integer - the required sum modulo 1073741824 (230).

Sample Input 1

Copy

2 2 2
 · · \n

Sample Output 1

Copy

20
  \n

Sample Input 2

Copy

4 4 4
 · · \n

Sample Output 2

Copy

328
   \n

Sample Input 3

Copy

10 10 10
  ·  ·  \n

Sample Output 3

Copy

11536
     \n

Hints

For the first example.
d(1 \cdot 1 \cdot 1)=d(1)=1; d(1 \cdot 1 \cdot 2)=d(2)=2; d(1 \cdot 2 \cdot 1)=d(2)=2; d(1 \cdot 2 \cdot 2)=d(4)=3; d(2 \cdot 1 \cdot 1)=d(2)=2; d(2 \cdot 1 \cdot 2)=d(4)=3; d(2 \cdot 2 \cdot 1)=d(4)=3; d(2 \cdot 2 \cdot 2)=d(8)=4.
So the result is 1+2+2+3+2+3+3+4=20.

Submit

请先登录

Submit

题解(0)