John Doe decided that some mathematical object must be named after him. So he invented the Doe graphs. The Doe graphs are a family of undirected graphs, each of them is characterized by a single non-negative number - its order.

We'll denote a graph of order k as D(k), and we'll denote the number of vertices in the graph D(k) as |D(k)|. Then let's define the Doe graphs as follows:
D(0) consists of a single vertex, that has number 1. D(1) consists of two vertices with numbers 1 and 2, connected by an edge. D(n) for n \ge 2 is obtained from graphs D(n-1) and D(n-2). D(n-1) and D(n-2) are joined in one graph, at that numbers of all vertices of graph D(n-2) increase by |D(n-1)| (for example, vertex number 1 of graph D(n-2) becomes vertex number 1+|D(n-1)|). After that two edges are added to the graph: the first one goes between vertices with numbers |D(n-1)| and |D(n-1)|+1, the second one goes between vertices with numbers |D(n-1)|+1 and 1. Note that the definition of graph D(n) implies, that D(n) is a connected graph, its vertices are numbered from 1 to |D(n)|. 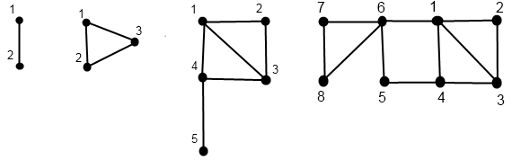The picture shows the Doe graphs of order 1, 2, 3 and 4, from left to right.
John thinks that Doe graphs are that great because for them exists a polynomial algorithm for the search of Hamiltonian path. However, your task is to answer queries of finding the shortest-length path between the vertices ai and bi in the graph D(n).

A path between a pair of vertices u and v in the graph is a sequence of vertices x1, x2, ..., xk (k \gt 1) such, that x1=u, xk=v, and for any i (i \lt k) vertices xi and xi+1 are connected by a graph edge. The length of path x1, x2, ..., xk is number (k-1).

The first line contains two integers t and n (1 \le t \le 105;1 \le n \le 103) - the number of queries and the order of the given graph. The i-th of the next t lines contains two integers ai and bi (1 \le ai,bi \le 1016, ai \neq bi) - numbers of two vertices in the i-th query. It is guaranteed that ai,bi \le |D(n)|.

Please, do not use the %lld specifier to read or write 64-bit integers in C++. It is preferred to use cin, cout streams or the %I64d specifier.

For each query print a single integer on a single line - the length of the shortest path between vertices ai and bi. Print the answers to the queries in the order, in which the queries are given in the input.