3947 - Limit - PK@Contest.bjtu

3947.Limit

Time Limit: 1s Memory Limit: 256MB

You are given two polynomials: P(x)=a0 \cdot xn+a1 \cdot xn-1+...+an-1 \cdot x+an and Q(x)=b0 \cdot xm+b1 \cdot xm-1+...+bm-1 \cdot x+bm. Calculate limit $3947_1.png$ .

Input Format(From the terminal/stdin)

Input The first line contains two space-separated integers n and m (0 \le n,m \le 100) - degrees of polynomials P(x) and Q(x) correspondingly.The second line contains n+1 space-separated integers - the factors of polynomial P(x): a0, a1, ..., an-1, an (-100 \le ai \le 100,a0 \neq 0).The third line contains m+1 space-separated integers - the factors of polynomial Q(x): b0, b1, ..., bm-1, bm (-100 \le bi \le 100,b0 \neq 0).

Output Format(To the terminal/stdout)

Output If the limit equals +∞, print "Infinity" (without quotes). If the limit equals -∞, print "-Infinity" (without the quotes).If the value of the limit equals zero, print "0/1" (without the quotes).Otherwise, print an irreducible fraction - the value of limit $3947_1.png$ , in the format "p/q" (without the quotes), where p is the - numerator, q (q \gt 0) is the denominator of the fraction.

Sample Input 1

Copy

2 1
1 1 1
2 5
 · \n
 · · \n
 · \n

Sample Output 1

Copy

Infinity
        \n

Sample Input 2

Copy

1 0
-1 3
2
 · \n
  · \n
 \n

Sample Output 2

Copy

-Infinity
         \n

Sample Input 3

Copy

0 1
1
1 0
 · \n
 \n
 · \n

Sample Output 3

Copy

0/1
   \n

Sample Input 4

Copy

2 2
2 1 6
4 5 -7
 · \n
 · · \n
 · ·  \n

Sample Output 4

Copy

1/2
   \n

Sample Input 5

Copy

1 1
9 0
-5 2
 · \n
 · \n
  · \n

Sample Output 5

Copy

-9/5
    \n

Hints

Let's consider all samples: 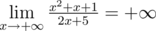$3947_2.png$ $3947_3.png$ $3947_4.png$ $3947_5.png$ $3947_6.png$ You can learn more about the definition and properties of limits if you follow the link: http://en.wikipedia.org/wiki/Limit_of_a_function

Submit

请先登录

Submit

题解(0)