You are given a directed graph G with n vertices and m arcs (multiple arcs and self-loops are allowed). You have to paint each vertex of the graph into one of the k (k \le n) colors in such way that for all arcs of the graph leading from a vertex u to vertex v, vertex v is painted with the next color of the color used to paint vertex u.The colors are numbered cyclically 1 through k. This means that for each color i (i \lt k) its next color is color i+1. In addition, the next color of color k is color 1. Note, that if k=1, then the next color for color 1 is again color 1.Your task is to find and print the largest possible value of k (k \le n) such that it's possible to color G as described above with k colors. Note that you don't necessarily use all the k colors (that is, for each color i there does not necessarily exist a vertex that is colored with color i).

Input The first line contains two space-separated integers n and m (1 \le n,m \le 105), denoting the number of vertices and the number of arcs of the given digraph, respectively.Then m lines follow, each line will contain two space-separated integers ai and bi (1 \le ai,bi \le n), which means that the i-th arc goes from vertex ai to vertex bi.Multiple arcs and self-loops are allowed.

Output Print a single integer - the maximum possible number of the colors that can be used to paint the digraph (i.e. k, as described in the problem statement). Note that the desired value of k must satisfy the inequality 1 \le k \le n.

For the first example, with k=2, this picture depicts the two colors (arrows denote the next color of that color). With k=2 a possible way to paint the graph is as follows. 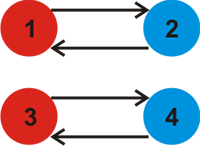It can be proven that no larger value for k exists for this test case.For the second example, here's the picture of the k=5 colors. 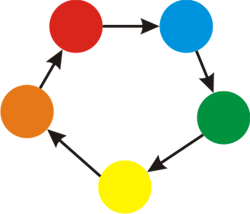A possible coloring of the graph is: 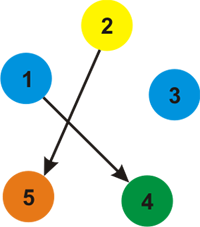For the third example, here's the picture of the k=3 colors. 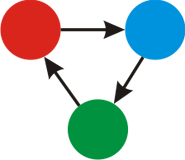A possible coloring of the graph is: