Polycarpus has recently got interested in sequences of pseudorandom numbers. He learned that many programming languages generate such sequences in a similar way: 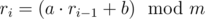(for i \ge 1). Here a, b, m are constants, fixed for the given realization of the pseudorandom numbers generator, r0 is the so-called randseed (this value can be set from the program using functions like RandSeed(r) or srand(n)), and 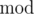denotes the operation of taking the remainder of division.For example, if a=2,b=6,m=12,r0=11, the generated sequence will be: 4,2,10,2,10,2,10,2,10,2,10,....Polycarpus realized that any such sequence will sooner or later form a cycle, but the cycle may occur not in the beginning, so there exist a preperiod and a period. The example above shows a preperiod equal to 1 and a period equal to 2.Your task is to find the period of a sequence defined by the given values of a,b,m and r0. Formally, you have to find such minimum positive integer t, for which exists such positive integer k, that for any i \ge k: ri=ri+t.

Input The single line of the input contains four integers a, b, m and r0 (1 \le m \le 105,0 \le a,b \le 1000,0 \le r0 \lt m), separated by single spaces.

Output Print a single integer - the period of the sequence.

The first sample is described above. In the second sample the sequence is (starting from the first element): 0,3,4,1,0,3,4,1,0,...In the third sample the sequence is (starting from the first element): 33,24,78,78,78,78,...