4248.Lucky Interval
Time Limit: 1s Memory Limit: 256MBPetya loves lucky numbers. We all know that lucky numbers are the positive integers whose decimal representations contain only the lucky digits 4 and 7. For example, numbers 47, 744, 4 are lucky and 5, 17, 467 are not.
One day Petya came across an interval of numbers [a,a+l-1]. Let F(x) be the number of lucky digits of number x. Find the minimum b (a \lt b) such, that F(a) = F(b), F(a+1) = F(b+1), ..., F(a+l-1) = F(b+l-1).
Input Format(From the terminal/stdin)
The single line contains two integers a and l (1 \le a,l \le 109) - the interval's first number and the interval's length correspondingly.
Output Format(To the terminal/stdout)
On the single line print number b - the answer to the problem.
Hints
Consider that [a,b] denotes an interval of integers; this interval includes the boundaries. That is, 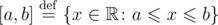
Submit
请先 登录