“codeplus比赛的时候在做什么？有没有空？能来解决丢番图方程问题吗？”sublinekelzrip这样问$qm$。

当然，$qm$并不会丢番图方程问题，所以sublinekelzrip改为提出了另一个题目，现在请你帮助$qm$解决这个题目。

这个问题是这样的：

若一个数列 $a$满足条件 $a_n=a_{n-1}+a_{n-2},n \geq 3$，而$a_1,a_2$为任意实数，则我们称这个数列为广义斐波那契数列。

现在请你求出满足条件 $a_1=i, a_2$为区间 $[l,r]$中的整数，且 $ a_k\ mod\ p=m$ 的广义斐波那契数列有多少个。

从标准输入读入数据。

本题包含多组数据，输入第一行包含一个正整数 $T$，表示数据组数。对于每组数据：

一行六个用空格隔开的整数 $i,l,r,k,p,m$，意义如「题目描述」所示。

输出到标准输出。

输出共 $T$行，每行一个数表示该组数据的答案。

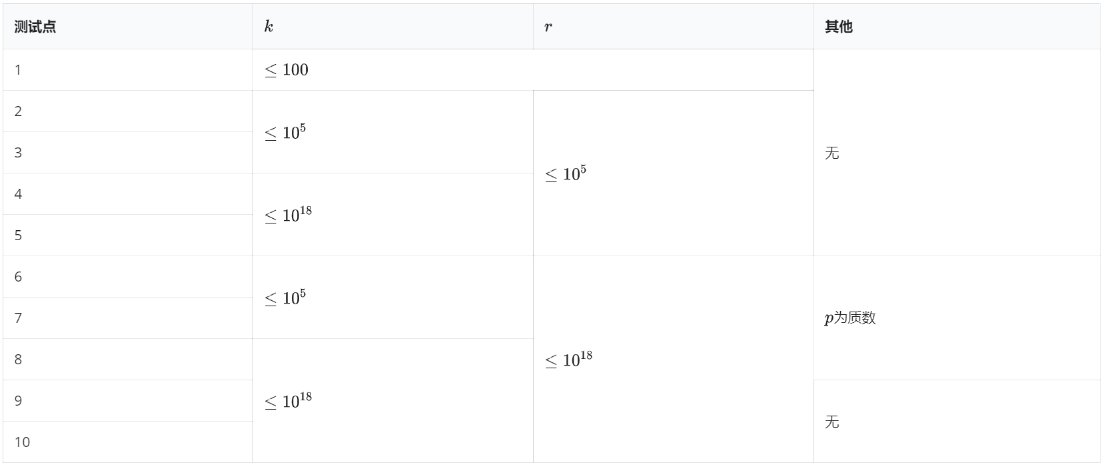
对于所有数据，$0≤l≤r, 1≤p≤10^9, 0≤m \lt p, T=10, 0≤i≤10^{18}, k≥3$。