三阶魔方是一款经典玩具，由26个小立方体（中心块6个、棱块12个、角块8个）组成，每个面都可以自由转动

捆绑魔方是由标准的三阶魔方将若干相邻的块捆绑粘合而成，这些捆绑的块无法被分离，使得魔方在旋转时可能会被阻挡，即每个面并非在任意时刻都能转动

下面给出捆绑魔方的还原状态实物图及其外表面平面展开图（捆绑方式是唯一的，所有的询问都使用这种魔方）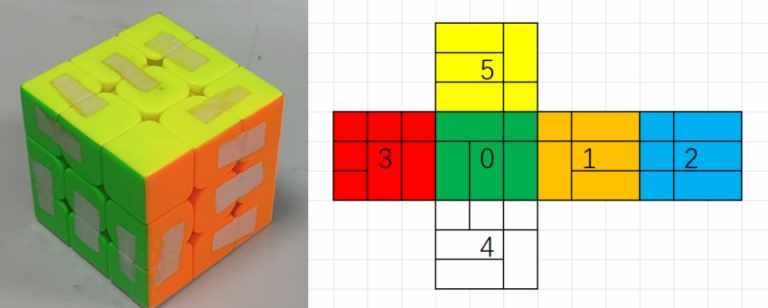

给你一个打乱后的捆绑魔方，请求解出还原所需的 最小 步数，并输出步数最少的操作序列中 字典序最小 的那个序列

每次操作，可以选择一个面并将其顺时针旋转90度 (请不要问为什么捆绑魔方只能顺时针旋转)

第一行包含一个正整数 $T(1≤T≤20)$表示测试用例组数。

对每组询问：以样例的格式，输入捆绑魔方打乱后的平面展开图。保证所有展开图的展开方式是相同的，且所有$6$个中心块在展开图中的对应位置不变。

简单来说，所有的输入为以下格式， 其中$0≤x≤5$，表示该部分的颜色

x x x
x 5 x
x x x
x x x x x x x x x x x x
x 3 x x 0 x x 1 x x 2 x
x x x x x x x x x x x x
x x x
x 4 x
x x x

保证给定状态合法且有解。

对每个询问，输出两行：

第一行输出一个整数$k$，表示还原所需最小操作步数。

第二行输出一个长度为 $k$ 的整数操作序列 $p_1,p_2,…,p_k(0≤pi≤5)$,表示对应的操作序列，其中 $p_i$ 表示：第$i$步操作为将中心块颜色为$p_i$的面顺时针旋转90度，两个操作之间以空格隔开。

若有多种操作序列满足步数最小，请输出其中字典序最小的序列。

样例1对应的实物图及展开图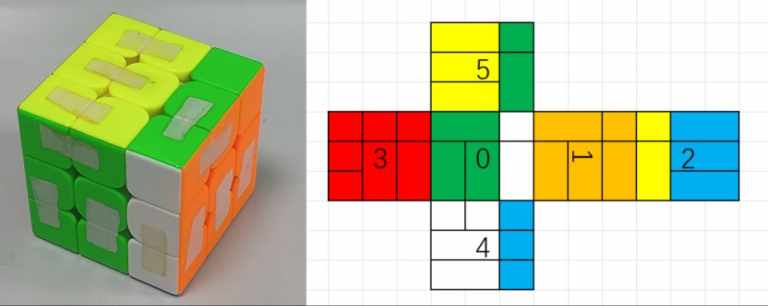

（此种状态下可行的合法操作为1， 2， 5，其余操作会被阻挡）

提示：该捆绑魔方共有1,108,800种不同的状态。

提供一个在线模拟操作传统三阶魔方的网站，仅供参考：https://rubiks-cube-solver.com/。