一天，学傻了的Yoshinow在学数论时，迷失在了数论的黑暗森林里！

（因为是在数论森林里！）现在Yoshinow得到了一棵树，现在他想知道：在某个以 $r$ 为根的子树内，有多少点对 $(i,j)$ ，满足 $i,j$ 的最小公倍数不超过 $x$（注意是编号的$lcm$）

由于Yoshinow非常——好奇，所以他现在一共有 $Q$ 个这样的询问。

形式化地说：给定 $n$ 个结点的有根树（以 $1$ 为根），结点标号从 $1$ 到 $n$ ，共有 $Q$ 次询问，每次询问给出两个参数 $r,x$ ，表示询问有多少点对 $(i,j)$，满足：

1. $i,j$ 是 $[1,n]$ 内的正整数。
2. $lcm(i,j)≤x$.
3. 标号为 $i,j$ 的结点均在以 $r$ 为根的子树内。

注：对于正整数$x,y$， $lcm(x,y)$ 表示 $x,y$ 的最小公倍数，即同时是 $x,y$ 倍数的最小正整数。例如，$10$ 和 $12$ 的最小公倍数是 $60$，即 $lcm(10,12)=60$.

第一行输入一个正整数 $T$，表示测试用例组数，$1≤T≤3$.

对每组询问：第一行输入一个整数$n$，其中$1≤n≤10^5$。

接下来 $n−1$ 行，每行两个整数 $u,v(1≤u,v≤n)$，表示 $u,v$ 之间有一条边。保证给出的 $n$ 个点构成树。

接下来一行一个整数$Q$，表示询问组数，$1≤Q≤10^6$.

接下来 $Q$ 行，每行两个整数 $r,x(1≤r≤n,0≤x≤10^5)$，表示一个询问。

共 $T$ 行，对每组测试用例，输出一行共 $Q$ 个整数，按顺序给出对应询问的答案，相邻整数用空格隔开。

样例给出的树如图所示：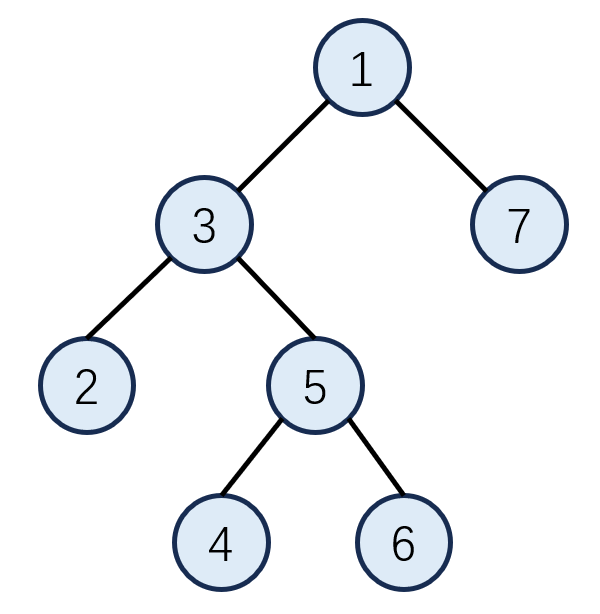

对于第一个询问，$r=3,x=23，r=3$ 的子树内共有 $5$ 个点，有 $5^2=25$ 对点对，除了 $(5,6),(6,5)$ 的最小公倍数是 $30>23$ 外，其余每个点对都满足最小公倍数不超过 $23$ 的条件，因此答案是 $25−2=23$.