4994.飞车狂飙
时间限制:1s 内存限制:256MB你现在正在筹备一场飞车比赛,众所周知,飞车比赛会同时有多辆车进行,因此赛道的设计十分关键。
现在你要修建由 $n$ 个赛道段组成的赛道,赛道会被铺设在一个无限大的二维平面网格上,每个赛道段占一个单元格。
一条合法的赛道需要满足如下条件:
- 赛道不能重叠,也就是相同的单元格上不能放置多个赛道段,因为重叠会使得赛车之间发生碰撞的概率提升。
- 赛道必须成环,因为飞车比赛的起终点是在同一点。
你现在让一位工人在平面上某个单元格的一条边上就位,并按照你给的预命令来进行修建赛道。预命令是一个长度为 $n$ 的仅包含 $LRS$ 的字符串,其中 $L$ 表示在他面向的单元格铺设一段相对于他面向的方向左转 $90$ 度的赛道,$R$ 表示在他面向的单元格铺设一段相对于他面向的方向右转 $90$ 度的赛道,$S$ 表示在他面向的单元格铺设一段相对于他面向的方向直行的赛道。之后,工人会顺着赛道来到下一条边上。
但你无法从你下达的预命令来看出赛道是否合法。现在你需要想办法判断它是否合法从而来指挥工人修建赛道。
输入格式(从终端/标准输入读取)
第一行一个整数 $T(1≤T≤10^4)$,表示测试数据组数。
对于每组数据,第一行一个整数 $n(1≤n≤10^5)$,表示轨道长度。第二行一个长为 $n$ 且仅由 $L,S,R$ 三种字符组成的字符串。
保证对于所有数据,满足 $∑n≤10^6$ 。
输出格式(输出至终端/标准输出)
对于每组数据,输出一个整数表示该字符串对应的预命令是否合法。
如果轨道存在重叠,输出 $−1$;如果轨道无重叠,但不成环,输出 $0$;如果轨道无重叠且成环,输出 $1$。
输入样例
复制
4 1 S 4 RRRR 10 LSLSLSSLSL 18 LSSLSLSLSSSRSRSSRR\n \n \n \n \n \n \n \n \n
输出样例
复制
0 1 0 -1\n \n \n \n
说明
样例中四条赛道如下图所示。其中蓝色线为初始时工人所在边,箭头朝向为初始时工人面向的方向。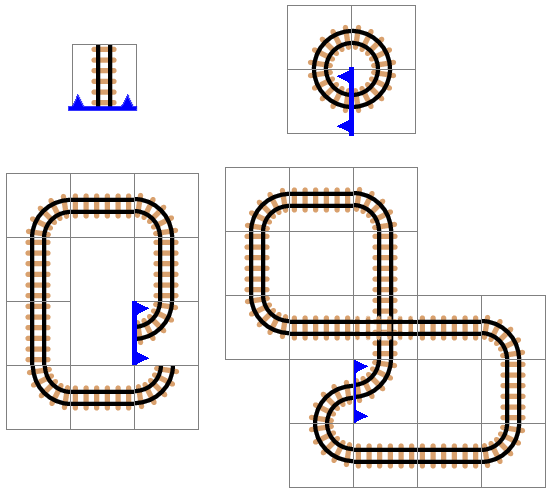
来源: 2024“钉耙编程”中国大学生算法设计超级联赛(6)
提交题解
Please login first.