Honeybee hives are typically divided into a brooding chamber and a superstructure, or super. The queen bee lays eggs only in the brooding chamber because a queen excluder prevents the queen from entering the super. Worker bees will produce honeycomb (hexagon networks made of beeswax) and honey to fill the honeycombs in both chambers.

A new species of honey bee, the ICPC bee, has a very unique, and not surprisingly, inefficient, way of building honeycombs. In each chamber, a single worker bee (the builder bee) is responsible for building the honeycomb that will hold the honey produced by all the other bees. This creates somewhat of a bottleneck because the other worker bees can not produce any honey in the chamber until at least one hexagonal cell of a honeycomb is built. The efficiency of honey production is dependent on how efficiently the builder bee does her job. If she jumps around and does not produce the honeycomb walls in an optimal way, honey production will suffer. A cell in a honeycomb is built one wall at-a-time by the builder bee and the cell is not considered complete until it is closed (has six sides). Each wall takes one hour to build. Note that some walls may be shared by two cells, in which case only the single wall is built.

A honeycomb that is $M$ cells wide by $N$ cells high consists of hexagonal cells as shown below for $M=4, N=6$ (note that the even rows have ($M-1$) cells:

If the builder bee wanted to make the other worker bees wait as long as possible by building the cell walls in an inefficient manner, what would be the maximum time in hours the worker bees would have to wait before they can start depositing honey in the first cell given an $M x N$ honeycomb structure? For example, consider a honeycomb structure where $M=2$ and $N=1$:

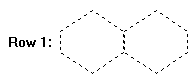
The dotted lines indicate where cell walls can be built. In this case, the maximum time it would take to make it so that no cell is complete is 10 hours, since there are 10 walls that can be built before any cell is complete. Building the final wall (the dotted line between the cells below), after 11 hours, would complete two cells, at which point the worker bees can fill them with honey.

Input consists of two space separated decimal integers, $M (2 ≤ M ≤ 1000000)$ and $N (1 ≤ N ≤ 1000000)$ which represents the width and height of the honeycomb structure to be built.

Output consists of a single integer value representing the maximum number of hours before the worker bees can begin depositing honey in the first completed cell.