A triangle △ABC is linked by a triangle △DEF if

1. Exactly one edge of △DEF passes through the interior of △ABC(in the plane of △ABC(see figure below)
   OR
2. One vertex of △DEF lies in the interior of △ABC (in the plane of △ABC) and the adjacent edges lie on opposite sides of the plane of △ABC

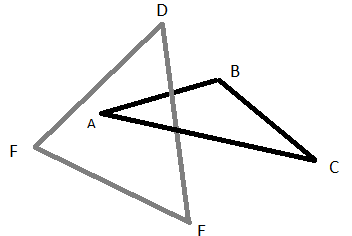
It turns out that △ABC is linked by △DEF if and only if △DEF is linked by △ABC. In this case we say that △ABC and △DEF are linked.

A set of points in 3-dimensional space is in general position, if no four points lie in the same plane(which means no three points lie on the same line).

It is known that given any six points in 3-dimensional space in general position, there is at least one way to split the six points into two sets of three so that the triangles determined by the two subsets are linked. Note that if the points are in general position, case 2 above can not occur because it would have four points in the plane of △ABC.

Write a program which takes as input six points in 3-dimensions and outputs the number of ways of splitting the points into two sets of three which give linked triangles as well as the points in the subsets.

Input consists of six lines containing three space separated double precision floating point values $x, y$ and $z$ giving the coordinates of a point, for six points in total. $(-10 \le x,y,z \le 10)$

The first line of output contains a single decimal integer $N$, which is the number of linked triangles found.

The first line is followed by $N$ additional lines each containing two space decimal integers, $m$ and $n$, for which choosing points $1$, $m$ and $n$ as one triangle and the remaining points as the other triangle give a linked pair. On each of these lines, $m$ < $n$, and the lines should be in lexicographical order.

That is (now pay attention), if $m1\ n1$ is above $m2\ n2$, then either $m1 \lt m2$ or ($m1 = m2$ and $n1 \lt n2$).