You're probably familiar with regular word searches, where you're presented with a grid of letters and a word to find. The word can be in a straight line horizontally, vertically, or diagonally (and perhaps backwards in any of those directions). For example, here is a grid of letters:

Figure 1. A word search grid

The word JAVA can be found going from the bottom right corner diagonally upwards.

In a kinky word search the path that spells out the word can have one or more kinks -- places where the path changes direction. For example, in the given grid you can spell the word PYTHON with $3$ kinks (one each at the T, H and O):

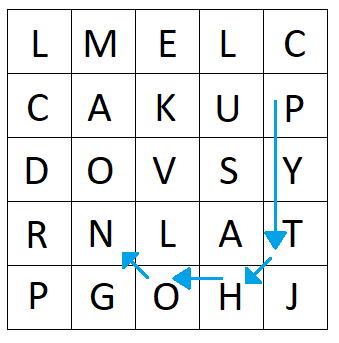
Figure 2. A kinky spelling of PYTHON

Adding kinks allows letters to be reused -- the word CPLUSPLUS can be found in the upper right corner of the grid (with $5$ kinks). However you cannot stay on a letter twice in a row, so you cannot spell the word HASKELL in this grid (though you can find at least $11$ more common programming languages). Your task is to see if the spelling of a word with a certain number of kinks is possible or not.

Input begins with a line containing two positive integers $r$ and $c$ ($r, c \leq 10)$, the number of rows and columns in the grid. After this are $r$ rows of $c$ uppercase characters. Letters are separated by a space. After the grid are two lines: The first line is an integer $k(k \le 2^{31}-1)$, the number of kinks. The second line contains an uppercase word to look for, with maximum length $100$.

Output either the word YES if it is possible to spell the given word with exactly $k$ kinks on the grid provided, or NO if it is not.