Dr. Hugh Klidd is a geometry expert who has recently become preoccupied with convex hulls. Recall that for a set of points in the $x\textrm{-}y$ plane, the convex hull is the smallest convex polygon containing all of those points. (A convex polygon has the property that for any two points on/in the polygon, the line segment connecting those two points lies entirely on/in the polygon.) Dr.~Klidd has just computed the convex hull of a set of $\textrm{points,}~S,$ which he denotes $H(S),$ and is quite pleased with the result:

• the convex hull has $n \geq 3$ vertices
• each vertex has integer coordinates
• no three of the convex hull vertices are collinear, i.e., lie on the same line

Dr.~Klidd is ambitious, though, so he wants this convex hull to grow. Specifically, he is looking for an extension point, which is a point $p=(x,y)$ satisfying the following conditions:

• $x$ and $y$ are integers
• if $S' = S \cup \{ p \}$ ($S$ with $p$ added), then the convex hull of $S',$ i.e., $H(S'),$ has $n+1$ vertices
• no three of these $n+1$ vertices are collinear

In other words, an extension point increases the number of convex hull vertices $\textrm{by}~1,$ while still keeping all its nice properties. For most convex hulls, $H(S),$ Dr.~Klidd can usually find at least one extension point, but he would like to know how many extension points there are to choose from. He postulates that there is an efficient way to count the number of extension points, but having never taken an algorithms course, he turns to you for help.

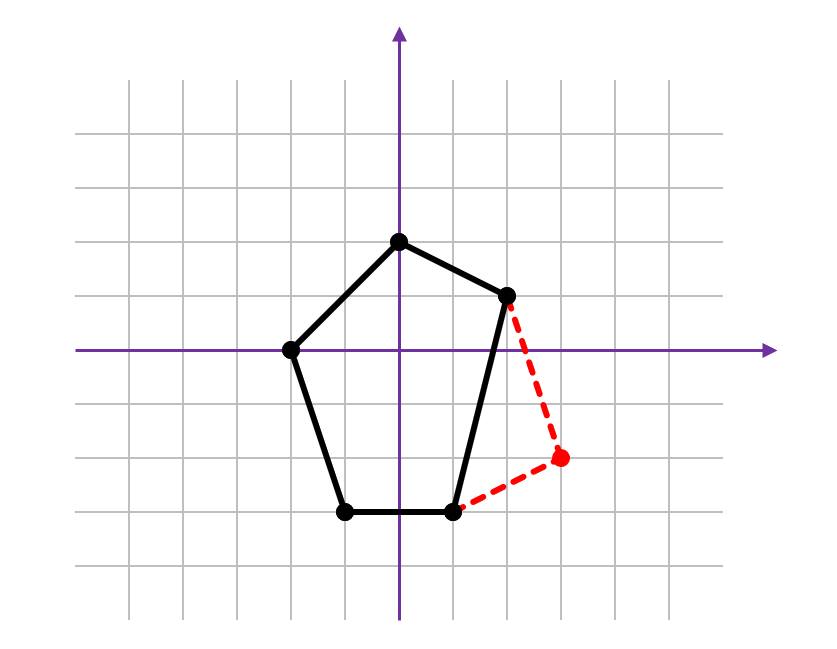
Figure 1. Illustration of an extension point for Sample Input~1

The first line of input contains an integer, $n,$ the number of vertices of the convex hull that Dr.~Klidd starts with $(3 \leq n \leq 50).$ This is followed by $n$ lines, each of which contains two space-separated integers, the $x$ and $y$ coordinates of one of the $n$ vertices $(-1\,000 \leq x,y \leq 1\,000).$ The $n$ points are distinct, no three are collinear, and they are given in counterclockwise order.

If the number of extension points for the convex hull specified in the input is infinite, output infinitely many. Otherwise, output the number of extension points.