Consider four integers $A$, $B$, $C$, and $D$, such that $A < B < C < D$. Let's put them in the corners of a square in some order and draw a loop $A - B - C - D - A$. Depending on the arrangement of the integers, we can get different loop shapes, but some arrangements produce the same shape:

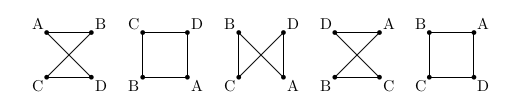
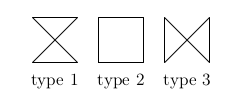
There are three possible loop shapes we can get:

Now consider an $n\times m$ matrix filled with distinct integers from $1$ to $nm$, inclusive. Each $2\times 2$ square in this matrix can be seen as a square with integers in its corners. Let's build a loop for each of these squares like we did before:

Your task is to perform the inverse operation. You are given the shape types for all $(n-1)(m-1)$ loops, and you need to build an $n\times m$ matrix filled with distinct integers from $1$ to $nm$, inclusive, that produces these shapes.

The first line contains two integers $n$ and $m$ ($2\le n, m\le 500$).

Each of the next $n-1$ lines contains a string of $m-1$ characters without spaces. Each character is a digit from $1$ to $3$, denoting the type of the shape of the corresponding loop.

Print an $n\times m$ matrix filled with distinct integers from $1$ to $nm$, inclusive, that produces the shapes of the loops in the input.

It can be shown that such a matrix always exists. If there are multiple answers, print any of them.