Let's say that three segments on a plane form a ${\it K-shaped figure}$ if:

• two of them share a common endpoint;
• this common endpoint lies strictly inside the third segment;
• these two segments are located on the same side with respect to the third one;
• all three segments are pairwise not collinear.

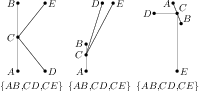
Figure 1. Valid K-shaped figures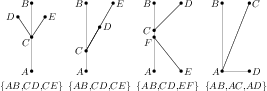

Figure 2. Invalid K-shaped figures

You are given a collection of $n$ segments on the plane. Find the number of triples of segments from this collection that form a K-shaped figure.

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \le t \le 3333$). The description of the test cases follows.

The first line of each test case contains a single integer $n$--- the number of segments ($3 \le n \le 1000$).

The $i$-th of the following $n$ lines contains four integers $x_{i,1}$, $y_{i,1}$, $x_{i,2}$, $y_{i,2}$--- the coordinates of endpoints of the $i$-th segment ($-10^6 \le x_{i,1}, y_{i,1}, x_{i,2}, y_{i,2} \le 10^6$). All segments have positive lengths. Some segments may coincide.

It is guaranteed that the sum of $n$ over all test cases does not exceed $10^4$.

For each test case, print a single integer--- the number of triples of segments that form a K-shaped figure.