Your task is to build a tower whose width is $2$ and height is $n$ . You have an unlimited supply of blocks whose width and height are integers.

For example, here are some possible solutions for $n=6$ :

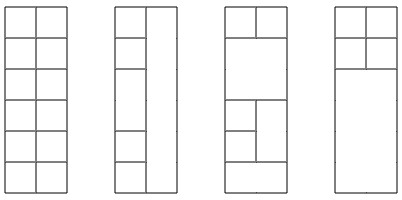
Given $n$ , how many different towers can you build? Mirrored and rotated towers are counted separately if they look different.

The first input line contains an integer $t$ : the number of tests.

After this, there are $t$ lines, and each line contains an integer $n$ : the height of the tower.

• $1 \le t \le 100$
• $1 \le n \le 10^6$

For each test, print the number of towers modulo $10^9+7$ .