6969.Grid Path Construction
Time Limit: 1s Memory Limit: 512MBGiven an $n \times m$ grid and two squares $a=(y_1,x_1)$ and $b=(y_2,x_2)$ , create a path from $a$ to $b$ that visits each square exactly once.
For example, here is a path from $a=(1,3)$ to $b=(3,6)$ in a $4 \times 7$ grid:
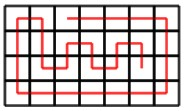
Input Format(From the terminal/stdin)
The first input line has an integer $t$ : the number of tests.
After this, there are $t$ lines that describe the tests. Each line has six integers $n$ , $m$ , $y_1$ , $x_1$ , $y_2$ and $x_2$ .
In all tests $1 \le y_1,y_2 \le n$ and $1 \le x_1,x_2 \le m$ . In addition, $y_1 \neq y_2$ or $x_1 \neq x_2$ .
- $1 \le t \le 100$
- $1 \le n \le 50$
- $1 \le m \le 50$
Output Format(To the terminal/stdout)
Print YES, if it is possible to construct a path, and NO otherwise.
If there is a path, also print its description which consists of characters U (up), D (down), L (left) and R (right). If there are several paths, you can print any of them.
Sample Input
5 1 3 1 1 1 3 1 3 1 2 1 3 2 2 1 1 2 2 2 2 1 1 2 1 4 7 1 3 3 6\n · · · · · \n · · · · · \n · · · · · \n · · · · · \n · · · · · \n
Sample Output special judge
YES RR NO NO YES RDL YES RRRRDDDLLLLLLUUURDDRURDRURD\n \n \n \n \n \n \n \n