为了下个版本挤进开荒车队，元素师正在重构她的阵盘……

阵盘以 $ n $ 个点为基础，且对于任意一对点 $ u,v~(1 \leq u < v \leq n) $ ，两点之间由以下四种结构(边)之一连接：

(A)：一条从 $ u $ 到 $ v $ 的水属性(蓝色)单向边和一条从 $ v $ 到 $ u $ 的火属性(红色)单向边；

(B)：一条从 $ u $ 到 $ v $ 的火属性(红色)单向边和一条从 $ v $ 到 $ u $ 的水属性(蓝色)单向边；

(C)：一条从 $ u $ 到 $ v $ 的暗属性(黑色)单向边和一条从 $ v $ 到 $ u $ 的暗属性(黑色)单向边；

(D)：一条从 $ u $ 到 $ v $ 的光属性(黄色)单向边和一条从 $ v $ 到 $ u $ 的光属性(黄色)单向边；

(也就是说你可以把阵盘当成一个 $ n $ 点无向边完全图)

元素师在战斗时会多次任意选择一条回路(解释见Hint)调动元素,释放出强大的魔法；然而魔法要讲究元素平衡, 否则阵盘中可能会存在一些危险回路：

(a)：经过火属性(红色)单向边但未经过水属性(蓝色)单向边的回路；

(b)：经过水属性(蓝色)单向边但未经过火属性(红色)单向边的回路；

(c)：只经过光属性(黄色)单向边而未经过其他三种单向边的回路；

(d)：只经过暗属性(黑色)单向边而未经过其他三种单向边的回路

————使用这些回路会引发大爆炸，并极大增加团灭的可能性。

现有 $ q $ 次询问，每次询问会给出一个 $ n $ ，代表阵盘的点数，而你需要告诉元素师：在 $ 4^{n(n-1)/2} $ 种构建阵盘的方案中，有多少种方案中不会出现任何危险回路，即 $ Ans_n $ ;

由于答案可能很大,请将 $ Ans_n $ 对 $ 998244353 $ 取模后再输出。

第一行含一个正整数 $ q~(1 \leq q \leq 5 \times 10^5) $ ，表示询问的次数。

接下来 $ q $ 行，每行有一个正整数 $ n~(1 \leq n \leq 10^7) $ ，表示所询问阵盘的点数。

对每组询问，输出一个非负整数独占一行，表示 $ Ans_n $ 对 $998244353$ 取模后的结果。

回路必须首尾相接，且不能原路折返；严谨点来说，设回路由 $ k $ 条边组成，每条边以 $ 1 \sim k $ 标号, 每条边的起点为 $ u_i $ ,终点为 $ v_i $ ,则一条回路合法当且仅当对于任意 $ 1 \leq i \leq k $ ，有 $ vi = u{i%k+1} $ 且 $ ui \neq v{i%k+1} $ 。(于是显然 $ k \geq 3 $ )

样例解释：

$ n=1 $ :没有选择,同时没有回路也算"不会出现任何危险回路";

$ n=2 $ :显然4种结构(边)都符合条件

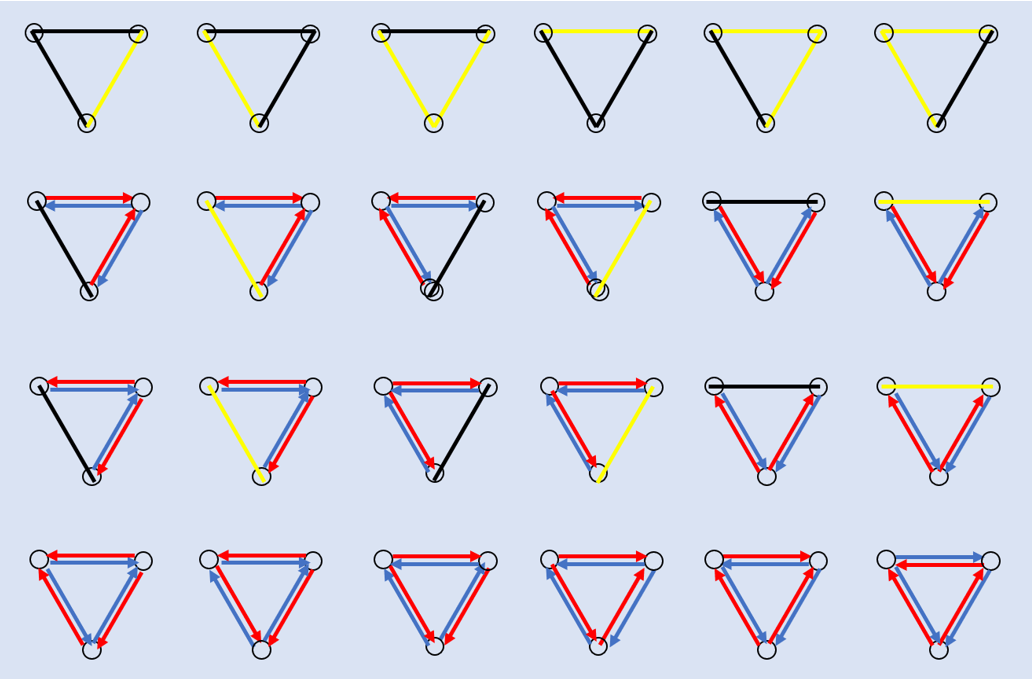
$ n=3 $ 的所有方案见下图: